| Krämer, M.: | Algebra II |
| Zeit und Ort: | Vorlesung: 4st, Do 10-12, H 20, Fr 10-12, H 18
Übungen: 2st, Do 14-16, S 78 |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 14. April 2005 |
| Inhalt: | In erster Linie einige algebraische Themen, die in den Staatsexamensklausuren immer mal wieder vorkommen, aber in der üblichen Algebra I im Allgemeinen keinen Platz haben: Ergänzungen zur Galoistheorie, Quadratische Reziprozitätsgesetz, Ideale in Zahlkörpern, Moduln über Hauptidealringen, Polynomringe in mehreren Variablen. Etwas Homologische Algebra. |
| für: | Hörer ab dem 4. Semester |
| Vorkenntnisse: | Lineare Algebra I, II; Algebra I |
| Schein: | ja |
| Literatur: | W. Müller: Algebra, Bayreuther Mathematische Schriften, Heft 57, 1999
Stoff aus diversen Algebrabüchern; Genaueres in der Vorlesung |
| Müller, W.: | Ring- und Modultheorie |
| Zeit und Ort: | Vorlesung: 3st, Di 14-15, S 80, Do 14-16, S 76
Übungen: 1st, Di 15-16, S 80 |
| Credit Points: | V 4,5 + Ü 1,5 |
| Beginn: | 12. April 2005 |
| Inhalt: | Halbeinfache Ringe, semiperfekte Ringe, Morita-Äquivalenz und Morita-Dualität |
| für: | Studierende der Mathematik ab 4. Fachsemester |
| Vorkenntnisse: | Algebra I |
| Schein: | ja (für Hauptprüfungen Diplom/Lehramt) |
| Literatur: | Kasch: Moduln und Ringe
Müller: Darstellungstheorie von endlichen Gruppen |
| Kerber, A.: | Codierungstheorie I |
| Zeit und Ort: | Vorlesung: 4st, Di 10-12, S 82, Do 10-12, S 80
Übungen: 2st, in zwei Gruppen 1. Gruppe: Mo 14-16, S 80 2. Gruppe: Mi 14-16, S 80 |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 12. April 2005 |
| Inhalt: | Grundbegriffe der algebraischen Codierungstheorie, also der Theorie und Anwendung fehlerkorrigierender linearer Codes (das sind endliche Vektorräume mit Hamming-Metrik) |
| für: | Studenten der Mathematik und Physik, sowie Lehramtsstudenten ab dem 5. Semester |
| Vorkenntnisse: | Lineare Algebra |
| Schein: | ja |
| Literatur: | Betten, Fripertinger, Kerber, Wassermann, Zimmermann: Codierungstheorie, Springer-Verlag (englische Fassung in Vorbereitung) |
| Catanese, F.: | Einführung in die Topologie |
| Zeit und Ort: | Vorlesung: 4st, Mo 14-16, Di 16-18, S 78
Übungen: 2st, Mi 14-16, S 78 |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 11. April 2005 |
| Inhalt: | A) Grundbegriffe der allgemeinen Topologie: Kompaktheit, Quotientenräume,..
B) Grundbegriffe der algebraischen Topologie und der Differentialtopologie, wie Fundamentalgruppe, Homologiegruppen .. mit mehr Betonung auf Eigenschaften und Anwendungen (z.B. Fixpunktsätze). C) Graphen, Bäume, Polynome, Zöpfe. |
| für: | alle Mathematikstudenten |
| Vorkenntnisse: | Lineare Algebra, Analysis I, II. |
| Schein: | ja |
| Literatur: | wird in der Vorlesung angegeben |
| Peternell, Th.: | Differentialgeometrie |
| Zeit und Ort: | Vorlesung: 4st, Mo, Di 10-12, H 16
Übungen: 2st, Di 14-16, H 20 |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 11. April 2005 |
| Inhalt: | Geometrie von Kurven und Flächen im dreidimensionalen Raum: Krümmung, Geodätische, globale Struktur von Kurven und Flächen; Riemannsche Geometrie: Metriken, Krümmung und deren geometrische Bedeutung. |
| für: | Studenten der Mathematik, Wirtschaftsmathematik, Technomathematik und Physik (Diplom und Lehramt) ab 5. Semester |
| Vorkenntnisse: | Analysis I, II; Lineare Algebra I, II |
| Schein: | ja |
| Literatur: | M. do Carma: Differentialgeometrie von Kurven und Flächen,
Viewegh weitere Literatur wird in der Vorlesung bekannt gegeben |
| Rein, G.: | Analysis IV (Funktionentheorie) |
| Zeit und Ort: | Vorlesung: 4st, Mo 10-12, H 17, Di 10-12, H 12
+ Fragestunde: 1st, nach Vereinbarung Übungen: 2st, in zwei Gruppen 1. Gruppe: Mo 14-16, H 19 2. Gruppe: Di 12.30-14, H 20 |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 11. April 2005 |
| Inhalt: | Im ersten Teil der Vorlesung wird die Integrationstheorie auf Untermannigfaltigkeiten
des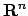 
behandelt. Untermannigfaltigkeiten sind die Verallgemeinerung von
Kurven und Flächen. Durch den sogenannten Differentialformen-Kalkül werden die in meiner
Vorlesung Analysis III elementar eingeführten Begriffe und Integralsätze abstrahiert und
verallgemeinert. Ziel ist der Stokes'sche Satz für Differentialformen, aus dem im
Spezialfall die ''elementaren'' Sätze von Gauß und Stokes der Analysis III folgen.
Der zweite Teil der Vorlesung gibt eine Einführung in die Funktionentheorie. Dies ist die Differential- und Integralrechnung von komplexwertigen Funktionen einer komplexen Variablen. Wie bereits in Analysis I-III gesehen, lassen sich viele Analysis-Resultate erst im Komplexen angemessen behandeln. Gleichzeitig gelten für Funktionen, die bzgl. einer komplexen Variablen differenzierbar sind, wesentlich stärkere Sätze als im reellen Fall. Dieser Teil der Vorlesung wird im WS 05/06 durch eine zweistündige Vorlesung fortgesetzt, damit insbesondere die LehramtsstudentInnen die im Staatsexamen geforderten Kenntnisse erwerben können. |
| für: | Mathematiker und Physiker ab 4. Semester |
| Vorkenntnisse: | Analysis I, II, III; Lineare Algebra I, II |
| Schein: | ja |
| Literatur: | wird am Ende der Vorlesung Analysis III bekannt gegeben |
| von Wahl, W.: | Funktionalanalysis II |
| Zeit und Ort: | Vorlesung: 4st, Di 12-14, S 80, Mi 10-12, S 82
Übungen: 2st, Mo 14-16, S 79 |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 12. April 2005 |
| Inhalt: | Banachräume, Selbstadjungierte Operatoren im Hilbertraum, Schrödinger-Operatoren, Spektralsatz und Anwendungen |
| für: | für Studierende der Mathematik und Physik ab 6. Semester |
| Vorkenntnisse: | Funktionalanalysis I |
| Schein: | ja |
| Literatur: | Skriptum, nähere Informationen unter:
http://www.uni-bayreuth.de/departments/math/org/mathe4/ mit3.html weitere Literatur wird in der Vorlesung bekannt gegeben |
| Lempio, F.: | Operations Research II |
| Zeit und Ort: | Vorlesung: 4st, Mo 10-12, H 20, Mi 8-10, H 20
+ Fragestunde: 1st, Mi 14-16, S 82 Übungen: 2st, in zwei Gruppen 1. Gruppe: Mi 12.30-14, S 82 2. Gruppe: Mi 16-18, S 82 |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 11. April 2005 |
| Inhalt: | Operations Research befasst sich mit der Modellierung, der qualitativen und
quantitativen Analyse und der algorithmischen Lösung von Entscheidungsproblemen.
Hauptanwendungsgebiete sind die Analyse und Optimierung vernetzter Systeme
in Wirtschaftsbetrieben, in der Städte- und Verkehrsplanung, in der Volkswirtschaft
und in der Technik. Von den zahlreichen hierbei eingesetzten mathematischen
Theorien und Verfahren wird eine Auswahl vorgestellt:
differenzierbare Optimierung, dynamische Optimierung, ganzzahlige und kombinatorische Optimierung. |
| für: | Mathematik-, Technomathematik und Wirtschaftsmathematikstudenten ab dem 6. Fachsemester; Lehramtsstudenten mit vertieftem Studienfach Mathematik; Studenten mit dem Nebenfach Mathematik; Studenten Betriebs- oder Volkswirtschaftslehre mit vertieften Mathematikkenntnissen |
| Vorkenntnisse: | Analysis I-III, Lineare Algebra I, II oder Mathematik für Physiker I-IV, Numerik I, II (kann auch parallel gehört werden), Programmierkurs |
| Schein: | ja |
| Literatur: | Die Grundlagen aus der numerischen Mathematik einschließlich der Theorie des
Simplexalgorithmus, des Transportalgorithmus und der Diskretisierung dynamischer Systeme
finden sich in:
Lempio, F.: Numerische Mathematik I: Methoden der Linearen Algebra, Bayreuther Mathematische Schriften, Band 51, 1997. Lempio, F.: Numerische Mathematik II: Methoden der Analysis, Bayreuther Mathematische Schriften, Band 55, 1998. Für die Einordnung in einen größeren Rahmen sind sehr nützlich: Zeidler, E. (ed.): Taschenbuch der Mathematik, 2. Auflage, Teubner, 2003. Grosche, G., Ziegler, V., Ziegler, D., Zeidler, E. (eds.): Taschenbuch der Mathematik II, 8. Auflage, Teubner, 2003. Weiterführende Literatur wird in der Vorlesung angegeben. |
| Rambau, J.: | Online-Optimierung |
| Zeit und Ort: | Vorlesung: 4st, Di 8-10, S 80, Mi 10-12, S 102
Übungen: 2st, nach Vereinbarung |
| Credit Points: | V 6 + Ü 3 |
| Beginn: | 12. April 2005 |
| Inhalt: | Warum kommt der Fahrstuhl erst so spät zu mir? Warum ist das ADAC-Hilfefahrzeug immer
noch nicht da? Warum bekomme ich die Webseite nur so langsam? Wann sollte ich eine
BahnCard kaufen, wenn ich noch nicht weiß, wann ich demnächst Bahn fahren werde?
Es gibt doch Optimierung und Operations Research, warum kann man diese Dienste nicht
einfach ''optimieren''?
Es zeigt sich immer wieder, dass Dienste dieser Art eine besondere Schwierigkeit bergen: sie müssen online optimiert werden, da man über zukünftige Aufträge - wenn überhaupt - nur stochastische Informationen hat. In dieser Vorlesung werden Algorithmen und Politiken für Online-Optimierungsprobleme vorgestellt und analysiert. Dabei ist es wichtig, was man eigentlich erreichen will: soll der Algorithmus im schlimmsten Fall noch etwas garantiert Vernünftiges liefern, oder soll er in der Erwartung gut sein, wenn man wenigstens stochastische Informationen hat. Diese Unterscheidung liefert mathematisch völlig unterschiedliche Konzepte, die beide ihre Vor- und Nachteile haben. In dieser Vorlesung haben Sie die Chance beide einführend kennen zu lernen. |
| für: | Studenten der Mathematik, Informatik und Wirtschaftsmathematik im Hauptstudium |
| Vorkenntnisse: | Lineare Algebra I, Analysis I, Grundkenntnisse der Stochastik |
| Schein: | ja |
| Literatur: | Borodin & El Yaniv: Online Optimierung
Bertsekas: Dynamic Programming and Optimal Control I+II |
| Rein, G.: | Gewöhnliche Differentialgleichungen |
| Zeit und Ort: | Vorlesung: 2st, Mi 8-10, H 9
Übungen: 1st, Mi 12-14 (14-tägig), H 11 |
| Credit Points: | V 3 + Ü 1,5 |
| Beginn: | 13. April 2005 |
| Inhalt: | Die Vorlesung setzt die Theorie der Gewöhnlichen Differentialgleichungen,
wie sie in meiner Analysis-Vorlesung begonnen wurde, fort. Neben Ergänzungen
zur Existenztheorie und zu linearen Differentialgleichungen wird insbesondere
die Stabilität von stationären Lösungen untersucht.
Die Vorlesung wird insbesondere den LehramtsstudentInnen empfohlen, da im Staatsexamen mehr Kenntnisse über Differentialgleichungen erwartet werden, als in den Grundvorlesungen behandelt werden können. |
| für: | Mathematiker und Physiker ab 4. Semester |
| Vorkenntnisse: | Analysis I, II, III; Lineare Algebra I, II |
| Schein: | ja |
| Literatur: | wird am Ende der Vorlesung Analysis III bekannt gegeben |
| Pesch, H-J.: | Singulär gestörte Differentialgleichungen |
| (siehe auch ''Veranstaltungen der Mathematik für Hörer anderer Fächer'') | |
| Zeit und Ort: | Vorlesung: 3st, Di 10-12, Do 14-15, S 103
Übungen: 1st, Do 15-16, S 103 |
| Credit Points: | V 4,5 + Ü 1,5 |
| Beginn: | 12. April 2005 |
| Inhalt: | Singulär gestörte Probleme sind Probleme, meist in Form von Anfangs- oder Randwertproblemen
für Differentialgleichungen, die von einem oder mehreren Parametern abhängen, so dass
die Lösungen nicht-gleichmäßige Konvergenz zeigen, wenn der oder die Parameter gegen (einen)
Grenzwert(e) streben, die vielleicht obendrein noch von besonderem Interesse sind. Die Natur
der nicht-gleichmäßigen Konvergenz kann von Problem zu Problem variieren. Man sucht eine
gleichmäßige Approximation für das nicht-gleichmäßige Verhalten, die einfach berechenbar ist.
Typische Anwendungsprobleme für ganz unterschiedliches Verhalten findet man bei der Untersuchung
der Stabilität unseres Sonnensystems oder bei physikalischen Problemen, bei denen
Grenzschichten auftreten, also ,,dünne`` Bereiche, in denen die Lösungen sich rapide
verändern.
Den genauen Inhalt der Vorlesung sowie eine detailliertere Zusammenfassung können Sie wie immer der Homepage unseres Lehrstuhls entnehmen: http://www.uni-bayreuth.de/departments/ingenieurmathematik/ LEHRE/vorlesungen_aktuell.html. |
| für: | alle mathematischen Studiengänge, insbesondere aber die Diplomstudiengänge Mathematik mit Nebenfach Physik, Technomathematik, sowie alle physikalischen Studiengänge, aber auch für interessierte Studierende ingenieurwissenschaftlicher Studiengänge, insbesondere mit Schwerpunkt in der Strömungsmechanik |
| Vorkenntnisse: | gute Kenntnisse der Analysis und Grundkenntnisse der gewöhnlichen Differentialgleichungen, ersatzweise Ingenieurmathematik, Mathematik für Physiker o. Ä. |
| Schein: | kein Schein |
| Literatur: | Die Vorlesung baut auf auf dem wunderbaren, leider vergriffenen Buch Singular Perturbation
Theory von Donald R. Smith, Cambridge University Press, 1985; siehe:
http://www.ams.org/mathscinet-getitem?mr=87d:34001 und http://www.emis.de/MATH-item?0567.34055 Vielleicht finden Sie noch ein antiquarisches Exemplar Weitere Literaturangaben werden auf der oben genannten Homepage und in der Vorlesung bekannt gegeben. |
| Chudej, K.: | Finite-Elemente-Methoden |
| (siehe auch ''Veranstaltungen der Mathematik für Hörer anderer Fächer'') | |
| Zeit und Ort: | Vorlesung: 3st, Di 8-10, Do 10-11.30, S 103
Übungen: 1st, nach Vereinbarung |
| Credit Points: | V 4,5 + Ü 1,5 |
| Beginn: | 12. April 2005 |
| Inhalt: | Viele, insbesondere technische, aber auch vermehrt wirtschaftswissenschaftliche Anwendungen
der Mathematik führen auf partielle Differentialgleichungen. Das heute oft gebrauchte
Schlagwort Simulation, im Sinne von Vorausberechnung technischer oder wirtschaftlicher
Prozesse, bedeutet meist nichts anderes als das Lösen von Differentialgleichungen auf dem
Rechner. Teure Experimente werden durch preiswerte numerische Rechnungen ersetzt. Komplexe
Vorgänge lassen sich analysieren und vorhersagen. Auch komplexe finanztheoretische
Zusammenhänge (Derivate) lassen sich mithilfe partieller Differentialgleichungen beschreiben
(Black-Scholes-Formel). In dieser Vorlesung steht die numerische Lösung von partiellen
Differentialgleichungen, insbesondere vom elliptischen Typus im Vordergrund. Nach einer
kurzen Einführung in die verschiedenen Typen partieller Differentialgleichungen
(hyperbolische, parabolische, elliptische partielle Differentialgleichungen) und die dazu
passenden Finite-Differenzen-Verfahren werden ausführlich Finite-Elemente-Verfahren für
elliptische partielle Differentialgleichungen besprochen. Die Vorlesung wird
höchstwahrscheinlich im nächsten Semester mit einem vom ersten Teil unabhängigen zweiten Teil
fortgesetzt, um auch iterative Verfahren zur Lösung größerer linearer Gleichungssysteme zu
behandeln, auf die letztendlich die Diskretisierung partieller Differentialgleichungen führt.
Den genauen Inhalt der Vorlesung sowie eine detailliertere Zusammenfassung können Sie wie immer der Homepage unseres Lehrstuhls entnehmen: http://www.uni-bayreuth.de/departments/ingenieurmathematik/ LEHRE/vorlesungen_aktuell.html |
| für: | alle mathematischen Studiengänge, alle physikalischen Studiengänge, interessierte Studierende ingenieurwissenschaftlicher oder geoökologischer Studiengänge |
| Vorkenntnisse: | gute Kenntnisse der Analysis und Grundkenntnisse der gewöhnlichen Differentialgleichungen, ersatzweise Ingenieurmathematik, Mathematik für Physiker o. Ä. |
| Schein: | kein Schein |
| Literatur: | Braess, D.: Finite Elemente, Springer, Berlin-Heidelberg-New York, 1991.
Hanke-Bourgeois, M.: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens, Kap. 16, Teubner, Wiesbaden, 2002. Jung, M. und Langer, U.: Methode der Finiten Elemente für Ingenieure, Eine Einführung in die numerischen Grundlagen und Computersimulation, Teubner, Wiesbaden, 2001. |